Laser Scanner 3D SkanDal Théorie
Sommaire
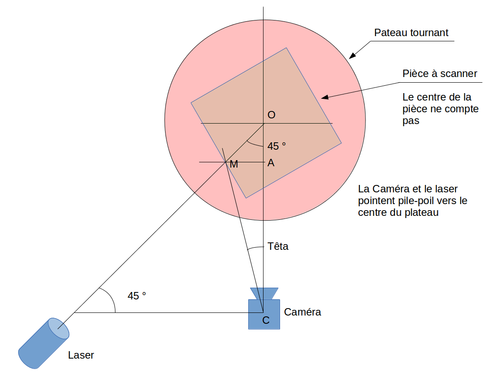
Vue de dessus
OM = AM / sin(Pi/4)
Vue camera et perspective
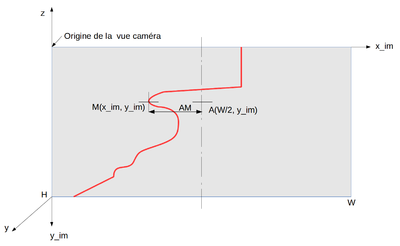
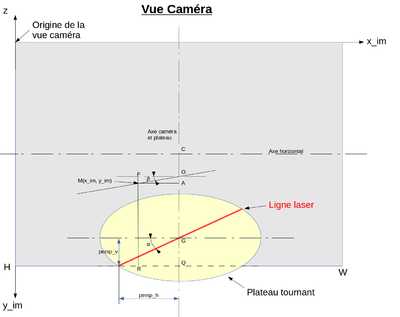
Vue caméra
Les coordonnées des points sont calculées dans un repère orthonormé, centré sur le point du centre sur le plateau, x et y axes horizontaux (sens et orientation sans importance, les calculs sont relatifs), z axe vertical.
OM = AM / sin(45°) donnera les x et y, z sera la hauteur du point dans la vue caméra corrigé de la perspective.
La caméra voit en perspective
Et non en orthonormé. Cela se traduit en particulier par la modélisation du plateau en cône si il n'y a pas de correction.
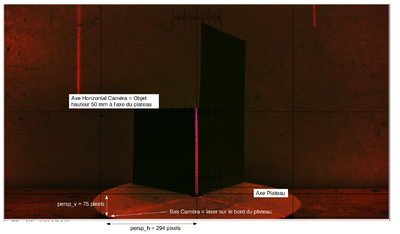
L'image est très foncée pour faire ressortir la ligne laser
Un point situé au bord du plateau de diamètre 100 mm est vu 75 pixels plus bas (avec une caméra 1280x800).
Un point situé à 50 mm de hauteur est vu en orthogonal: pas de correction.
Un point situé à une hauteur de 100 mm et à 50 mm de l'axe sera vu 75 pixels plus haut.
OpenCV Perspective
OpenCV permet de faire une transformation sur l'image. Mais il faut définir la matrice de transformation, alors que la solution ci-dessous est plus simple.
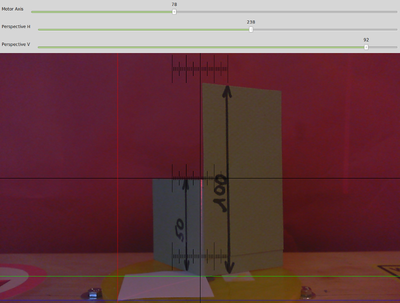
Mesure de la perspective avec opencv
Des Sliders dans la vue caméra permettent de définir une ligne horizontale bleue et une ligne verticale rouge. L'intersection de ces lignes doit tomber pile poil sur l'intersection de la ligne laser et le bord du plateau. La perspective est calculée automatiquement et d'enregistrée dans le fichier de configuration scan.ini.
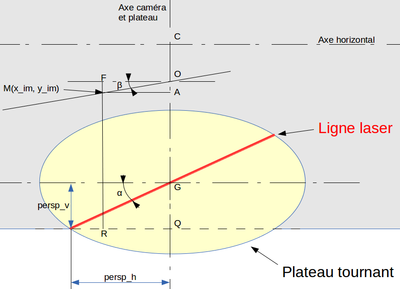
Calcul de la correction de la perspective
La caméra est positionnée précisément par rapport à l'objet.
Soit un point M de la ligne laser sur l'image caméra, coordonnées (x_im, y_im) avec l'origine en haut à gauche.
- x_im, y_im connu
Ce qui est connu dans scan.ini
- width
- height
- z_down = GQ en pixels, les points en dessous sont supprimés, ils ne devraient pas exister.
- persp_h = 259.0
- persp_v = 71.0
d'où tang(alpha) = persp_v / persp_h connu
Nous cherchons la coordonnées z du point M dans l'espace: z = GO
Big Bang
Soit M(x_im, y_im)
- AM = width/2 - x_im
- FM = height - y_im
L'angle beta = angle de perspective du point M:
- beta = alpha si M est sur le plateau
- beta = 0 si M est sur l'axe horizontal caméra, donc M est à 50 mm de hauteur du plateau
- beta = - alpha si M est à 100 mm du plateau
Dans un repère orthonormé avec une origine en C, la correction verticale est proportionnelle à beta.
Soit pos_vert_x = position de M par rapport à C = height/2 - y_im
- tg(beta) = a * CA + b
Si A en C, AC = CC = 0:
- 0 = a * CC + b => 0 = a * 0 + b => b = 0
Si A au bord du plateau, A = Q,
- tg(alpha) = a * CQ = a * (-height/2) # Origine en C, Q est vers le bas
Soit
- a = tg(alpha) / (height/2)
- a = 2 * tg(alpha) / height
Résumé du calcul de la hauteur d'un point
- AM = width/2 - x_im
- FM = height - y_im
- x_vert = (height / 2) - y_im
- a = -2 * tg_alpha / height
- tg_beta = a * x_vert
- z = FM + AM * tg(beta)
Avec ce calcul, la modélisation du plateau , la modélisation d'un CD sont plates. Un cube est bien cubique ! CQFD !
Avec ce calcul enfin clair, il est évident que z_down est théoriquement égal à persp_v ! Nous laissons ce paramètre, en pratique la théorie peut-être assez loin de la pratique. Sheldon ne peut pas comprendre ça !
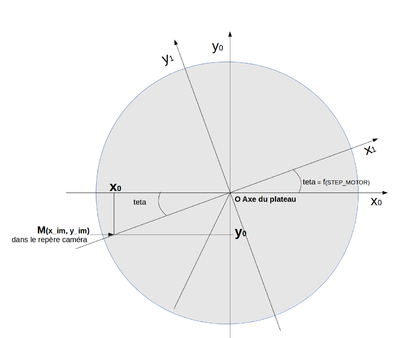
Changement de repère orthonormé
Calcul des coordonnées x0, y0 d'un points de l'image M et du numéro de step moteur.
Le plateau fait un tour complet pour un scan, soit 360° en un nombre de pas = STEP_MOTOR
alpha = numéro de frame * ( 2 * Pi / STEP_MOTOR )
Au premier paragraphe, nous avons obtenu: la positon de M par rapport à O dans l'image
OM = AM / sin(Pi/4)
x0 = OM * sin(teta)
y0 = OM * cos(teta)
Distorsion de la vue caméra
Camera calibration With OpenCV
Des caméras ont été autour pendant un long temps. Cependant, avec l'introduction des caméras cachées bon marché à la fin du 20e siècle, ils sont devenus un phénomène courant dans notre vie quotidienne. Malheureusement, ce bon marché est livré avec son prix: une distorsion importante. Heureusement, ceux-ci sont des constantes et avec un calibrage et une certaine reconfiguration nous pouvons corriger cela. En outre, à l'étalonnage, vous pouvez également déterminer la relation entre les unités de la caméra naturelles (pixels) et les unités réelles du monde (par exemple millimètres).
Ceci n'a pas été pris en compte