Oscillation simple
Sommaire
Description
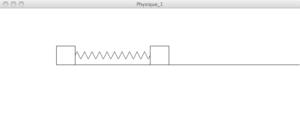
L'idée de cette première partie est de réaliser la simulation d'un mobile sur coussin d'air relié par un ressort à un point fixe.
Construction de l'environnement
int deplacement = 150;
void setup() {
size(800, 300, P2D);
smooth();
frameRate(60);
}
void draw() {
background(255);
fill(255);
translate(deplacement, deplacement);
rect(0, -50, 50, 50);
line(0, 0, 1020, 0);
}
Ajout des classes
Nous avons donc figuré le plan où le mobile va se déplacer ainsi que le point d'appui du ressort. Pour la suite, nous allons construire deux classes, une pour le ressort et une autre pour le mobile.
Le mobile est caractérisé par sa position sur l'axe. Nous aurions pu simplement n'utiliser qu'une valeur x pour le mobile, mais comme l'objectif est de l'améliorer dans le futur, nous allons utilisé un PVector.
class Mobile {
PVector position;
Mobile (PVector pos) {
position = pos;
}
}
Pour le ressort nous allons créer une classe Ressort qui se caractérise par son point d'ancrage, par le point où est accroché le mobile, sa constante de raideur et sa longueur au repos lorsqu'il n'est soumis à aucune force.
class Ressort {
PVector pointAncre;
Mobile pointMobile;
float longueurRepos = 200; // longueur au repos en pixel
float forceK = 5; // Constant de raideur en N.m-1
Ressort(PVector pointA, Mobile pointB) {
pointAncre = pointA;
pointMobile = pointB;
}
}
Maintenant il faut instancer ces classes dans le programme principal et les initialiser.
Ressort ressort;
Mobile mobile;
int deplacement = 150;
void setup() {
size(800, 300, P2D);
smooth();
frameRate(60);
mobile = new Mobile(new PVector(250, -25));
ressort = new Ressort(new PVector(50, -25), mobile);
}
Pour pouvoir faire apparaître ces objets que nous venons de créer, il faut est nécessaire de créer des méthodes répondant à cette tâche. Le mobile n'est composé que d'un rectangle, ajouter ces lignes dans la classe Mobile :
void afficher() {
rect(position.x, position.y - 25, 50, 50);
}
Le ressort est un peu plus complexe à simuler. Nous prenons le parti d'un ressort à 10 spires et chaque spire composée d'un zigzag réalisé à l'aide de vertex. Plus le ressort est comprimé plus l'intervalle de chaque spire est réduit. Ajouter ces lignes à la classe Ressort
void afficher() {
float intervalle = (pointMobile.position.x - pointAncre.x) / 10;
for (int i = 0; i < 10; i++) { // 10 spires de ressort
noFill();
beginShape();
vertex(pointAncre.x + intervalle * i, -25);
vertex(pointAncre.x + intervalle * i + intervalle / 4, -35);
vertex(pointAncre.x + intervalle * i + 3 * intervalle / 4, -15);
vertex(pointAncre.x + intervalle * i + intervalle, -25);
endShape();
}
}
Il ne reste plus qu'à les afficher par ces méthodes dans la méthode draw du programme principal.
mobile.afficher();
ressort.afficher();
Mise en oeuvre de l'intéractivité
Avant de passer au calcul des forces, nous allons ajouter un peu d'interactivité, pour pouvoir déplacer le mobile avec la souris. Une première méthode de la classe Mobile permet de sélectionner le mobile si le bouton de la souris est cliquer et que le souris est au dessus du mobile. Nous introduisons aussi une nouvelle variable couleur qui permet de voir le mobile une fois sélectionner. La variable selectionRef permet de stocker la distance entre la souris le point de référence du mobile.
void selectionner(PVector PMouse) {
if ((PMouse.x > deplacement + position.x) && (PMouse.x < deplacement + position.x + 50) && (PMouse.y > deplacement + position.y - 25) && (PMouse.y < deplacement + position.y + 25)) {
selection = true;
selectionRef = PVector.sub(position, PMouse);
couleur = color(100);
}
}
PVector selectionRef;
color couleur = color(255);
boolean selection = false;
Il faut maintenant modifier la méthode afficher pour prendre en compte le changement de couleur du mobile :
void afficher() {
fill(couleur);
rect(position.x, position.y - 25, 50, 50);
}
Ajouter la méthode suivante dans le programme principal, pour permettre les interruptions de la souris.
void mousePressed() {
mobile.selectionner(new PVector(mouseX, mouseY));
}
La méthode suivante toujours dans le programme principal a pour objectif de faire appel à la méthode de désélection du mobile lorsque le bouton de la souris est relâchée.
void mouseReleased() {
mobile.deSelectionner();
}
Cette méthode de la classe Mobile change simplement la couleur du mobile.
void deSelectionner() {
selection = false;
couleur = color(255);
}
Maintenant nous pouvons créer une méthode de la classe Mobile pour permettre de glisser le mobile avec le curseur de la souris.
void glisser(PVector PMouse) {
if (selection) {
position = PVector.add(selectionRef, PMouse);
if (position.x < 70) { // limite de compression du ressort
position.x = 70;
}
position.y = -25; // impose le déplacement sur l'axe des X
}
}
Pour visualiser les déplacements, il faut faire appel à cette méthode dans le programme principal. Insérer ces lignes avant les méthodes d'affichage.
PVector souris = new PVector(mouseX, mouseY);
mobile.glisser(souris);
A présent le mobile bouge au rythme de la souris mais n'est pas du tout soumis à la force du ressort.
Mise en oeuvre de la force de rappel
Pour le cas d'un ressort la force résultante est proportionnelle à son allongement relatif<ref>Forces élastiques</ref>. Donc nous allons créer une méthode pour la classe Ressort qui calcule cette force.
void calculForce() {
PVector rappel = PVector.sub(pointMobile.position, pointAncre); // Vecteur du déplacement
float longueur = rappel.mag();
float etirement = longueur - longueurRepos; // Calcul de l'étirement
rappel.normalize();
rappel.mult((-1) * forceK * etirement / correction); // Calcul de la force de rappel
pointMobile.force = rappel;
}
Nous avons introduit une variable "correction" dans la méthode Ressort parce qu'il faut faire correspondre le nombre de pixel en mètre de déplacement. Ce nombre est empirique et il faudrait regarder de manière plus pousser cette relation( à faire).
int correction = 60;
Dans la méthode Mobile, il faut introduire une variable "force" et l'initialiser. Cette variable prendra la valeur de toute les forces qui feront bouger le mobile.
PVector force = new PVector(0, 0);
Dans le programme principal, il faut faire calculer à chaque frame la force résultante de l'action du ressort.
ressort.calculForce();
Mise en oeuvre du déplacement en fonction des forces
Pour calculer les positions successives du mobile en fonction du temps et des forces qui agissent sur lui, nous utilisons l'intégration Verlet<ref>Intégration Verlet </ref> qui permet de simuler au mieux ceci. Intégration Verlet x(t+1) = 2 * x(t) - x(t-1) + a * ∆T * ∆T Pour effectuer ce calcul il nous faut intégrer la position précédente du mobile par la variable positionPrec qui sera un PVector, il faut aussi l'initialiser dans le constructeur de la class Mobile.
positionPrec = pos;
Pour le calcul de la nouvelle position du mobile nous allons créer une méthode, actualiser() pour le réaliser. Nous passons le ∆T en paramètre. Pour la calcul de la nouvelle position, nous utilisons une variable temporaire calcul. Pour déterminer l'accélération, il faut utiliser la deuxième loi de Newton<ref>Soit un corps de masse m (constante) : l'accélération subie par ce corps dans un référentiel galiléen est proportionnelle à la résultante des forces qu'il subit, et inversement proportionnelle à sa masse m. Lien</ref>. A = F / M. Auparavant il faut déclarer et initialiser la variable masse pour les besoins du calcul. Nous prenons toujours garde que la position lors de la compression reste dans la limite du ressort.
void actualiser(float deltaT) {
PVector calcul = PVector.mult(position, 2); // Intégration Verlet x(t+1) = 2 * x(t) - x(t-1) + a * ∆T * ∆T
calcul.sub(positionPrec);
PVector acceleration = PVector.div(force, masse); // Loi de Newton : F = M * A
acceleration.mult(deltaT * deltaT);
calcul.add(acceleration);
positionPrec = position.get();
position = calcul.get();
if (position.x < 70) {
position.x = 70; // Limite minimale de compression du ressort
}
}
Pour finir, il faut appeler cette dernière méthode dans le programme principal après le calcul des forces après avoir déclarer et initialiser la variable delta.
Script Processing principal
//-----------------------------------------------------------------------------
// Projet : La physique amusante
// Programme : Physique_1.pde
// Auteur : Sylvain Blocquaux
// Date : 11 avril 2011
// Version : 1.0
//-----------------------------------------------------------------------------
Ressort ressort;
Mobile mobile;
int deplacement = 150;
float delta;
void setup() {
size(800, 300, P2D);
smooth();
frameRate(60);
delta = 1 / frameRate;
mobile = new Mobile(new PVector(250, -25));
ressort = new Ressort(new PVector(50, -25), mobile);
}
void draw() {
background(255);
fill(255);
translate(deplacement, deplacement);
rect(0, -50, 50, 50);
line(0, 0, 1020, 0);
PVector souris = new PVector(mouseX, mouseY);
mobile.glisser(souris);
ressort.calculForce();
mobile.actualiser(delta);
mobile.afficher();
ressort.afficher();
}
void mousePressed() {
mobile.selectionner(new PVector(mouseX, mouseY));
}
void mouseReleased() {
mobile.deSelectionner();
}
Script Processing class Mobile
//-----------------------------------------------------------------------------
// Projet : La physique amusante
// Classe : Mobile.pde
// Auteur : Sylvain Blocquaux
// Date : 11 avril 2011
// Version : 1.0
//-----------------------------------------------------------------------------
class Mobile {
PVector position;
PVector positionPrec;
PVector selectionRef;
color couleur = color(255);
boolean selection = false;
PVector force = new PVector(0, 0);
float masse = 0.5; // Masse en kg
Mobile (PVector pos) {
position = pos;
positionPrec = pos;
}
void afficher() {
fill(couleur);
rect(position.x, position.y - 25, 50, 50);
}
void actualiser(float deltaT) {
PVector calcul = PVector.mult(position, 2); // Intégration Verlet x(t+1) = 2 * x(t) - x(t-1) + a * ∆T * ∆T
calcul.sub(positionPrec);
PVector acceleration = PVector.div(force, masse); // Loi de Newton : F = M * A
acceleration.mult(deltaT * deltaT);
calcul.add(acceleration);
positionPrec = position.get();
position = calcul.get();
if (position.x < 70) {
position.x = 70; // Limite minimale de compression du ressort
}
}
void selectionner(PVector PMouse) {
if ((PMouse.x > deplacement + position.x) && (PMouse.x < deplacement + position.x + 50) && (PMouse.y > deplacement + position.y - 25) && (PMouse.y < deplacement + position.y + 25)) {
selection = true;
selectionRef = PVector.sub(position, PMouse);
couleur = color(100);
}
}
void glisser(PVector PMouse) {
if (selection) {
position = PVector.add(selectionRef, PMouse);
if (position.x < 70) { // limite de compression du ressort
position.x = 70;
}
position.y = -25; // impose le déplacement sur l'axe des X
}
}
void deSelectionner() {
selection = false;
couleur = color(255);
}
}
Script Processing class Ressort
//-----------------------------------------------------------------------------
// Projet : La physique amusante
// Classe : Ressort.pde
// Auteur : Sylvain Blocquaux
// Date : 11 avril 2011
// Version : 1.0
//-----------------------------------------------------------------------------
class Ressort {
PVector pointAncre; Mobile pointMobile; float longueurRepos = 200; // longueur au repos en pixel float forceK = 5; // Constant de raideur en N.m-1 int correction = 60;
Ressort(PVector pointA, Mobile pointB) {
pointAncre = pointA;
pointMobile = pointB;
}
void calculForce() {
PVector rappel = PVector.sub(pointMobile.position, pointAncre); // Vecteur du déplacement
float longueur = rappel.mag();
float etirement = longueur - longueurRepos; // Calcul de l'étirement
rappel.normalize();
rappel.mult((-1) * forceK * etirement / correction); // Calcul de la force de rappel
pointMobile.force = rappel;
}
void afficher() {
float intervalle = (pointMobile.position.x - pointAncre.x) / 10;
for (int i = 0; i < 10; i++) { // 10 spires de ressort
noFill();
beginShape();
vertex(pointAncre.x + intervalle * i, -25);
vertex(pointAncre.x + intervalle * i + intervalle / 4, -35);
vertex(pointAncre.x + intervalle * i + 3 * intervalle / 4, -15);
vertex(pointAncre.x + intervalle * i + intervalle, -25);
endShape();
}
}
} </source>