Objets récursif

Objets récursif

Pour modifier la page utiliser l'onglet Modifier avec formulaire.

Résumé	Utiliser les capacités d'OpenSCAD afin de réaliser des volumes récursif, voir même fractal.
Auteur(s)	Bjorn
Licence	CC-BY-SA 3
Date de création	07 juillet 2017

Intentions / Contexte

OpenSCAD est un outil de conception 3D paramétrique basé sur un langage suffisamment développé pour permettre de créer des algorithmes générant des objets à notre place.
La récursivité est permise par le logiciel (sous conditions, on y reviendra) et ceci ouvre le champ à la création d'objets fractals.

Principe de fonctionnement

Rédaction en cours...

Besoins / Compétences

- Un ordinateur avec OpenSCAD installé
- Des connaissances sur OpenSCAD
- Maîtriser le concept d'Algorithme récursif

Mise en œuvre

Concept général : arrêt de la récursion

OpenSCAD vous fait rapidement savoir quand votre calcul est infini, il faut donc prévoir une condition d'arrêt. Si l'on construit l'objet en diminuant à chaque itération la taille de l'élément, taille du plus petit élément souhaité semble une bonne option. Sinon prévoir un compteur global avec un nombre d’itération maximum est une sécurité.

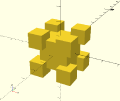
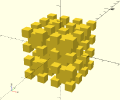
Cube de Cube de Cube (etc.)

Pas une fractale à proprement parler, c'est essentiellement un test "simple" pour valider le fonctionnement de la récursion sur le logiciel.
L'idée est de créer une fonction créant un cube de taille t et de centre [x,y,z], puis de se rappeler en communicant comme taille t/2 et comme centre les cordonnées de chaque sommet du cube précédemment créé.
La variable scale est la taille du cube de la première itération, min_rec est la taille du plus petit cube formé.

scale = 20;
min_rec = 2;
rec_cube(scale, [0,0,0]);
module rec_cube(local_scale){
    if(local_scale>min_rec){
        cube(local_scale,center=true);
        translate([local_scale/2,local_scale/2,local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([-local_scale/2,local_scale/2,local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([local_scale/2,-local_scale/2,local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([local_scale/2,local_scale/2,-local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([-local_scale/2,-local_scale/2,local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([-local_scale/2,local_scale/2,-local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([local_scale/2,-local_scale/2,-local_scale/2]){
            rec_cube(local_scale/2);
        };
        translate([-local_scale/2,-local_scale/2,-local_scale/2]){
            rec_cube(local_scale/2);
        };
    }
}

• 

  Itération 1

• 

  Itération 2

• 

  Itération 3

• 

  Itération 4

Éponge de Menger

Wikipedia présente très bien l'éponge_de_Menger, enfin beaucoup mieux que je ne pourrais le faire moi-même.
L'idée générale de algorithme de construction est une différence entre un cube de dimension max et de l'ensemble des "croix" de dimension 3. Le truc pas très classe c'est que chaque itération est appelé 20 fois.
C'est un peu lourd, la compilation en pâtit...

scale = 20;
min_rec = 6;
difference()
{
    cube(scale,center=true);
    rec_cube(scale, [0,0,0]);
};

module rec_cube(local_scale){
    if(local_scale>min_rec){
        tiers_scale = local_scale/3;
        cube([local_scale,tiers_scale,tiers_scale],center=true);
        cube([tiers_scale,local_scale,tiers_scale],center=true);
        cube([tiers_scale,tiers_scale,local_scale],center=true);
        translate([tiers_scale,tiers_scale,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,-tiers_scale,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,tiers_scale,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,-tiers_scale,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,tiers_scale,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,-tiers_scale,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,tiers_scale,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,-tiers_scale,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([0,tiers_scale,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,0,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,tiers_scale,0]){
            rec_cube(tiers_scale);
        };
        translate([0,-tiers_scale,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,0,tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,-tiers_scale,0]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,0,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,tiers_scale,0]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,-tiers_scale,0]){
            rec_cube(tiers_scale);
        };
        translate([tiers_scale,0,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([0,-tiers_scale,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([-tiers_scale,0,-tiers_scale]){
            rec_cube(tiers_scale);
        };
        translate([0,tiers_scale,-tiers_scale]){
            rec_cube(tiers_scale);
        };
    }
}

Rédaction en cours...